#Simplifying a polyline/polygon

Polylines and polygons can be simplified to save storage space or bandwidth.

phpgeo provides two implementations for simplifying polyline/polygons.

The first implementation uses the Ramer–Douglas–Peucker algorithm (also known as Douglas-Peucker algorithm). The other implementation examines the bearings of the segments and removes a segment when its bearing angle is similar to the bearing angle of its predecessor segment. I named it the Delta-Bearing algorithm.

#Ramer-Douglas-Peucker Algorithm

<?php

use Location\Coordinate;
use Location\Formatter\Coordinate\DecimalDegrees;
use Location\Polyline;
use Location\Processor\Polyline\SimplifyDouglasPeucker;

$polyline = new Polyline();
$polyline->addPoint(new Coordinate(10.0, 10.0));
$polyline->addPoint(new Coordinate(20.0, 20.0));
$polyline->addPoint(new Coordinate(30.0, 10.0));

$processor = new SimplifyDouglasPeucker(1500000);

$simplified = $processor->simplify($polyline);

foreach ($simplified->getPoints() as $point) {
    echo $point->format(new DecimalDegrees()) . PHP_EOL;
}

The example code will remove all points which perpendicular distance is less than 1,500,000 meters (1,500 km) from the surrounding points.

The code above produces the output below:

10.00000 10.00000
30.00000 10.00000

#Delta-Bearing Algorithm

<?php

use Location\Coordinate;
use Location\Formatter\Coordinate\DecimalDegrees;
use Location\Polyline;
use Location\Processor\Polyline\SimplifyBearing;

$polyline = new Polyline();
$polyline->addPoint(new Coordinate(10.0, 10.0));
$polyline->addPoint(new Coordinate(20.0, 20.0));
$polyline->addPoint(new Coordinate(30.0, 10.0));

$processor = new SimplifyBearing(90);

$simplified = $processor->simplify($polyline);

foreach ($simplified->getPoints() as $point) {
    echo $point->format(new DecimalDegrees()) . PHP_EOL;
}

The constructor argument for the SimplifyBearing class is the minimum required angle in degrees between two adjacent polyline segments so that no points will be removed. If the bearing angle difference is less that the given value, the middle point will be removed from the resulting polyline.

The code above produces the output below:

10.00000 10.00000
30.00000 10.00000

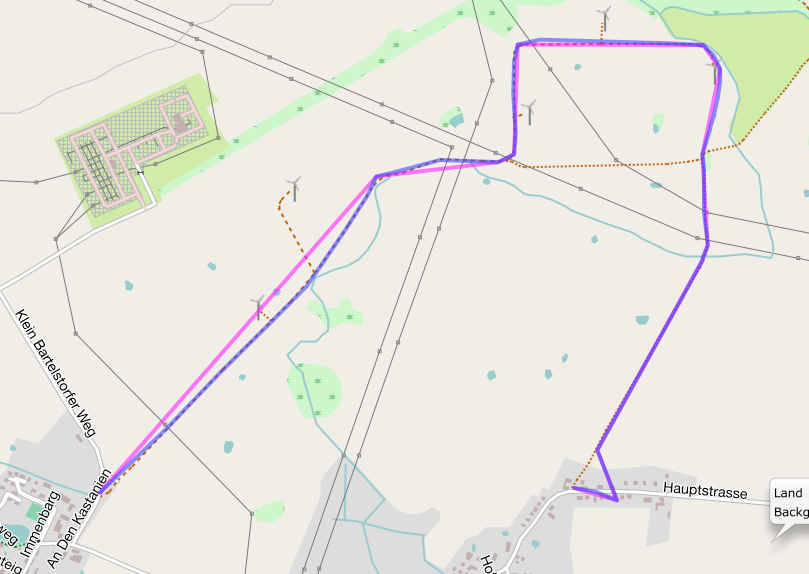
The following image shows both a polyline and its simplified version. The simplification was done with the Delta-Bearing Algorithm with a threshold angle of 20 degrees. The original polyline is painted in blue, the simplified polyline is magenta.